
In this blog we will try to get the basic idea behind reinforcement learning and understand what is a multi arm bandit problem. We will also be trying to maximise CTR(click through rate) for advertisements for a advertising agency.
Article includes:
1. Basics of reinforcement learning
2. Types of problems in reinforcement learning
3. Understamding multi-arm bandit problem
4. Basics of conditional probability and Thompson sampling
5. Optimizing ads CTR using Thompson sampling in R
Reinforcement Learning Basics
Reinforcement learning refers to goal-oriented algorithms, which learn how to attain a complex objective (goal) or maximise along a particular dimension over many steps; for example, maximise the points won in a game over many moves. They can start from a blank slate, and under the right conditions, they achieve superhuman performance. Like a child incentivized by spankings and candy, these algorithms are penalized when they make the wrong decisions and rewarded when they make the right ones — this is reinforcement.
Reinforcement Learning is the science of making optimal decisions.
Let us understand this by an example. Suppose there is a robot which is learning to walk. If it takes a big step, it will fall down. Next time if it takes a smaller step then it is able to hold the balance. The robot tries variations like this many times and learns to walk steadily. The robot has succeeded.
What we see here is called reinforcement learning. It directly connects a robot’s action with an outcome, without the robot having to learn a complex relationship between its activities and results. The robot learns how to walk based on reward (staying on balance) and punishment (falling). This feedback is considered “reinforcement” for doing or not doing an action.
How is reinforcement learning different from machine learning?
Machine learning is often split between three main types of learning: supervised learning, unsupervised learning, and reinforcement learning.
The Big Picture
The type of learning is defined by the problem you want to solve and is intrinsic to the goal of your analysis:
- You have a target, a value or a class to predict. For instance, let’s say you want to predict the revenue of a store from different inputs (day of the week, advertising, promotion). Then your model will be trained on historical data and use them to forecast future revenues. Hence the model is supervised, it knows what to learn.
- You have unlabelled data and looks for patterns, groups in these data. For example, you want to cluster to clients according to the type of products they order, how often they purchase your product, their last visit, … Instead of doing it manually, unsupervised machine learning will automatically discriminate between different clients.
- You want to attain an objective. For example, you want to find the best strategy to win a game with specified rules. Once these rules are specified, reinforcement learning techniques will play this game many times to find the best strategy.
Reinforcement learning algorithms try to find the best ways to earn the greatest reward. Rewards can be winning a game, earning more money or beating other opponents. They present state-of-art results on very human task, for instance. There are three basic concepts in reinforcement learning: state, action, and reward.
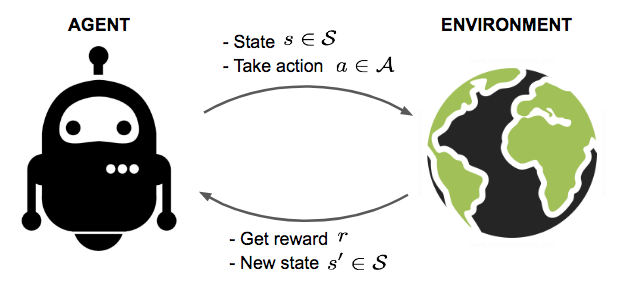
- Agent
It is an actor which interacts with the environment and accomplishes the task. In the previous example, the robot which is learning to walk is the agent - State
The state describes the current situation. For a robot that is learning to walk, the state is the position of its two legs. - Action
The action is what an agent can do in each state. Given the state, or positions of its two legs, a robot can take steps within a certain distance. There are typically finite (or a fixed range of) actions an agent can take. For example, a robot stride can only be, say, 0.01 meter to 1 meter. - Reward
When a robot takes an action in a state, it receives a reward. Here the term “reward” is an abstract concept that describes feedback from the environment. A reward can be positive or negative. When the reward is positive, it is corresponding to our normal meaning of reward. When the reward is negative, it is corresponding to what we usually call “punishment.”
There are generally 3 fundamental problems we deal with in the reinforcement learning.
-
The problem of exploration versus exploitation
The exploration-exploitation trade-off is a fundamental dilemma whenever you learn about the world by trying things out. The dilemma is between choosing what you know and getting something close to what you expect (‘exploitation’) and choosing something you aren’t sure about and possibly learning more (‘exploration’).
Exploration is related to global search as well as exploitation is related to local search. In the first one, we are interested in exploring the search space looking for good solutions, whereas in the second one we want to refine the solution and try to avoid big jumps on the search space.
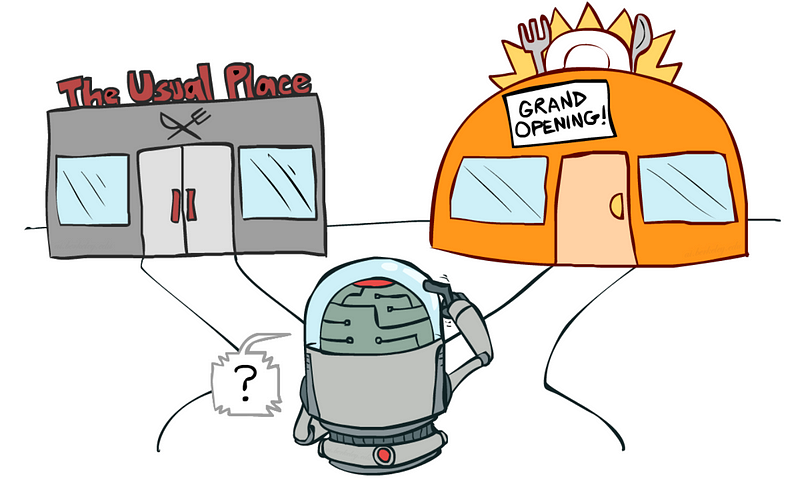
Example: Suppose you are at your favourite food joint which serves you your favourite chicken burger whose taste you are quite familiar with. One day, you find some other restaurants nearby who also serve your favourite chicken burger. What will you do here? Will you stay with the previous restaurant and have your burger whose taste you are quite sure of (exploitation) or you try out a different restaurant (exploration) only to realise that they server much better burgers as compared to previous one.
2. The problem of delayed reward
“Real” reinforcement learning, or the version used as a machine learning method today, concerns itself with the long-term reward, not just the immediate reward.

The long-term reward is learned when an agent interacts with an environment through many trials and errors. The robot that is running through the maze remembers every wall it hits. In the end, it remembers the previous actions that lead to dead ends. It also remembers the path (that is, a sequence of actions) that leads it successfully through the maze. The essential goal of reinforcement learning is learning a sequence of actions that lead to a long-term reward. An agent learns that sequence by interacting with the environment and observing the rewards in every state.
3. Generalisation problems
There will be many learning problems in the world in which going through every possible state is not possible. Suppose in the previous example if instead of 3 or 4, you have an option of exploring 2,000,000 other restaurants, will you be able to visit every possible restaurant? Maybe not. Maybe you will try to generalize them using different criteria, for example, saying restaurants in region A serves better burgers than restaurants in region B. Here we are generalizing some of the states (visiting a restaurant) which we may not actually visit ever or are even hidden.
In this article, we will be focusing on the problem based on exploration vs exploitation. One such problem is Multi-arm bandit problem.
What is a multi-arm bandit problem?
The multi-armed bandit problem is a classic problem that well demonstrates the exploration vs exploitation dilemma. Imagine you are in a casino facing multiple slot machines and each is configured with an unknown probability of how likely you can get a reward for one play. The question is: What is the best strategy to achieve the highest long-term rewards?
They are called “bandits” as these machines at casino loot away money from the people in most of the cases.
A naive approach can be that you continue playing with one machine for many many rounds so as to eventually estimate the “true” reward probability according to the law of large numbers. However, this is quite wasteful and surely does not guarantee the best long-term reward.
Multi-Armed Bandit Example
- A news website has to make a decision about which articles to display to a visitor. With no information about the visitor, all click outcomes are unknown. The first question is, which articles will get the most clicks? And in which order should they appear? The website’s goal is to maximise engagement, but they have many pieces of content from which to choose, and they lack data that would help them to pursue a specific strategy\
- A drug company needs to provide the best medicine to set of patients. The company needs to find the best set of patients for the particular drug and at the same time making sure of the case that it is wrongly administered to as a small set of people as possible
Defining a multi-arm bandit problem
A Bernoulli multi-armed bandit can be described as a tuple of ⟨A, R⟩, where:
- We have K machines with reward probabilities, {θ1,…,θK}.
- At each time step t, we take an action an on one slot machine and receive a reward r.
- A is a set of actions, each referring to the interaction with one slot machine. The value of action a is the expected reward, Q(a)=E[r|a]=θ. If action a at the time step t is on the sixth machine, then Q(at)=θi.
- R is a reward function. In the case of Bernoulli bandit, we observe a reward r in a stochastic fashion. At the time step t, rt=(at)rt=R(at) may return reward 1 with a probability Q(at)Q(at) or 0 otherwise.
3 Strategies to solve multi-arm bandit problem
- No exploration/Random Selection
Here we may select any slot machine at random and obtain a reward from it. This is the most naive and bad approach - Exploration at random
In this case, we try to explore first by trying out different slot machines and then shift to an exploitation mode based upon rewards received from our exploration. While doing constant exploitation, we keep a small probability aside for selecting some other slot machine rather than current winner to look for better rewards - Exploration smartly with preference to uncertainty
Rather than leaving the exploration mode completely in hands of a fixed probability value, we calculate smartly the probability of exploring the options rather than exploiting them
Thompson Sampling as a solution to multi-arm bandit problem
In artificial intelligence, Thompson sampling named is a heuristic for choosing actions that addresses the exploration-exploitation dilemma in the multi-armed bandit problem. It consists in choosing the action that maximises the expected reward with respect to a randomly drawn belief.
Before understanding the core concepts of Thompson sampling, it will be really helpful to revise some basic concepts of conditional probability.
Conditional probability is the probability of one event occurring with some relationship to one or more other events.

Bayes theorem is a formula that describes how to update the probabilities of hypotheses when given evidence. It follows simply from the axioms of conditional probability but can be used to powerfully reason about a wide range of problems involving belief updates.
Given a hypothesis H and evidence E, Bayes theorem states that the relationship between the probability of the hypothesis before getting the evidence and the probability of the hypothesis after getting the evidence.
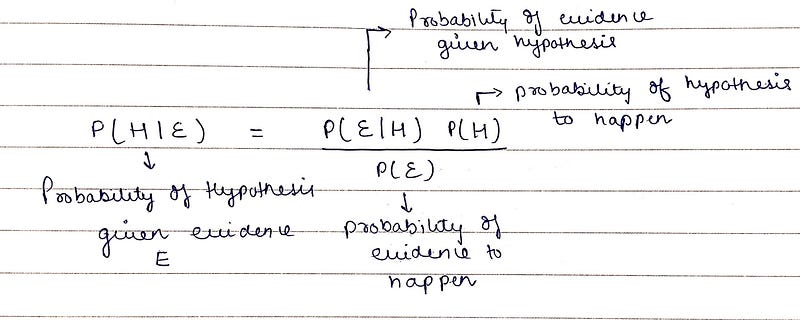
Thompson sampling follows bayesian statistics very closely. Let us directly dive into components of Thompson sampling.
Consider a set of contexts X, a set of Actions A (pulling the arm of a slot machine) and rewards received as R(0 for losing money/1 for winning the lottery). In each round, an agent/player chooses from a set of actions(which slot machine`s arm it should pull) and receives a corresponding reward R(1: Agent wins the lottery by performing the action an on the specific slot machine,0: Agent loses money in that action performed). The aim of the agent is to play such actions so that it maximizes the cumulative rewards.
Basic components in Thompson sampling are
Likelihood function
Likelihood function determines what is the most suitable distribution of rewards for a given slot machine.
Prior Belief Distribution
Prior belief can be stated as the belief we have on a given slot machine that it will produce a winning reward. Rewards observed over different probability values of prior belief of a given slot machine is known as prior belief distribution.

Posterior Belief Distribution
It is also a beta distribution which is relieved after multiplying the likelihood function with prior belief distribution. Posterior belief refers to updated prior belief (after conducting more actions of pulling arms of slot machines) that a given slot machine will produce a winning reward.
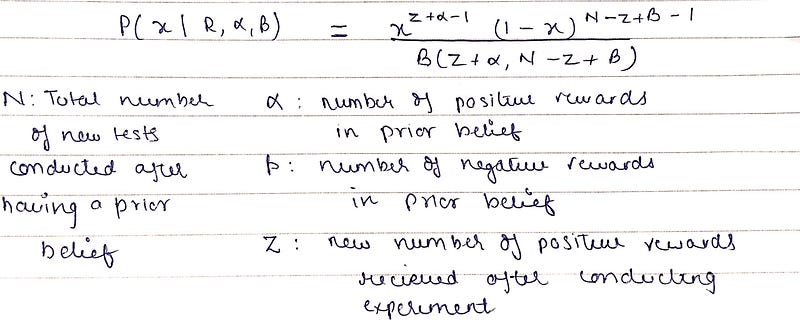
Thompson sampling is generally of the form of

Example
Suppose we as a team belong to an archaeological department wherein we dig up ancient artefacts and try to determine their age. Our job is to try and pinpoint what year(s) the place was likely inhabited. In probability terms, we want to work out forp(inhabited) a range of years. As we uncover relics like pottery and coins, we use that evidence to refine our beliefs about when the village was inhabited.
Our prior belief, in this case, can be the inhabitance period of the people who used this pottery.

Likelihood function can be taken as the existence of pottery(manufacturing) during the inhabitance period.

Our posterior belief of inhabitance of village given we have found a pottery from there.

Posterior belief is calculated by multiplying prior belief distribution with likelihood distribution given the evidence.

Thompson Sampling Algorithm to solve MAB

Implementation in R to solve MAB problem
Problem Statement
An advertising agency has 10 different ads which they want to show to their users. Agency wants to find the add which will get the clients of the agency highest conversion. We need to help the agency in finding the most suited add to maximize the conversions through them.
Code implementation
##################### Thompson Sampling ############################
# Importing the dataset
dataset = read.csv('Ads_CTR_Optimisation.csv')
# Implementing Thompson Sampling
N = 10000 ## Number of total trials
d = 10 ## Number of processes
ads_selected = integer(0)
numbers_of_rewards_1 = integer(d) ### Number of 1 rewards received from dataset
numbers_of_rewards_0 = integer(d) ### Number of 0 rewards received from dataset
total_reward = 0
for (n in 1:N) {
ad = 0
max_random = 0
for (i in 1:d) {
### We create a beta distribution for every ad here and take any 1 random point from it
random_beta = rbeta(n = 1,
shape1 = numbers_of_rewards_1[i] + 1,
shape2 = numbers_of_rewards_0[i] + 1)
### Selecting the add which is further away from 0 since we are placing one with better distribution to
### at extreme end
if (random_beta > max_random) {
max_random = random_beta
ad = i
}
}
ads_selected = append(ads_selected, ad) ## Storing which add was selected
reward = dataset[n, ad] ## Storing reward for the add we selected
#### Dividing rewards into 1s and 0s to to plot the beta distribution
if (reward == 1) {
numbers_of_rewards_1[ad] = numbers_of_rewards_1[ad] + 1
} else {
numbers_of_rewards_0[ad] = numbers_of_rewards_0[ad] + 1
}
total_reward = total_reward + reward ## Calculating total rewards
}
# Visualising the results
hist(ads_selected,
col = 'blue',
main = 'Histogram of ads selections',
xlab = 'Ads',
ylab = 'Number of times each ad was selected')
Output
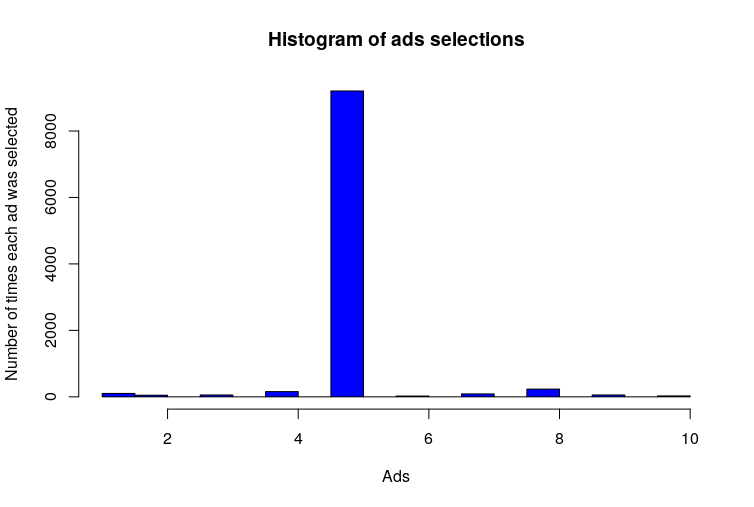
Using Thompson sampling it was observed that selected ad 5 is capable of maximising conversions for the client of the ad agency. The cumulative reward for the ad 5 is much more than any other reward. Congratulations, we were able to finally help news agency in selecting the best ad to display to users in an optimised manner.
